카테고리 없음
Math Problem No.1 (자작)
Silver Hat
2022. 3. 8. 21:28
앞으로 이와 같은 내용은 모두 이 티스토리 블로그에 쓸 예정이다.
네이버랑 글이 겹치는 경우는 ps 카테고리밖에 없을 것이니 여긴 아니다.
(티스토리에서의 수식 작성은 처음이라 수식 상태가 개발이다; 수식 공부를 해야 한다)
(이 글은 PC에서 접속해야 가독성이 높다)

우선 처음 나온
또한

지금까지의 내용을 그림으로 표현하면 대략 이렇다.
왼쪽 경계는 점점 높아지고, 오른쪽 경계는 점점 낮아지며 직선이 점점 눕는 형태다.
단,
이제 더 이상 할 수 있는 게 없으므로 다음으로 넘어간다.

=> 어떤 구간에서
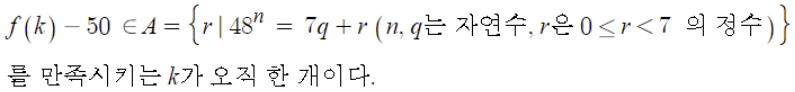
더보기
^n) 이 성립한다.
이 성립한다.
(49-1)(49-1)\cdots&space;) 에서 49와 -1에 대한 식으로 전개하면
에서 49와 -1에 대한 식으로 전개하면 ^{k}) 이다.
이다.
이 때 49를 포함한 항은 모두 7의 배수이기 때문에
49를 포함한 모든 항을 (
( 는 자연수) 라고 나타내면 위 시그마 식은
는 자연수) 라고 나타내면 위 시그마 식은 ^n&space;) 이다.
이다.
여기서 이 홀수이면
이 홀수이면  이므로 7로 나눈 나머지가 6, 짝수이면
이므로 7로 나눈 나머지가 6, 짝수이면  이므로 나머지가 1이다.
이므로 나머지가 1이다.
따라서 로 가능한 값은 1과 6이다.
로 가능한 값은 1과 6이다.
이 때 49를 포함한 항은 모두 7의 배수이기 때문에
49를 포함한 모든 항을
여기서
따라서
=>
정리를 해보자.
그리고
i)  과만 만나는 경우
과만 만나는 경우
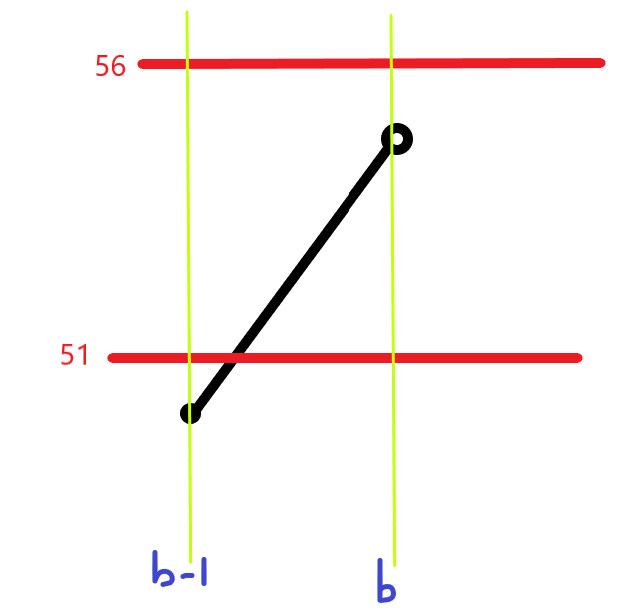
두 식을 연립하자.
우선
따라서
ii)  과만 만나는 경우
과만 만나는 경우
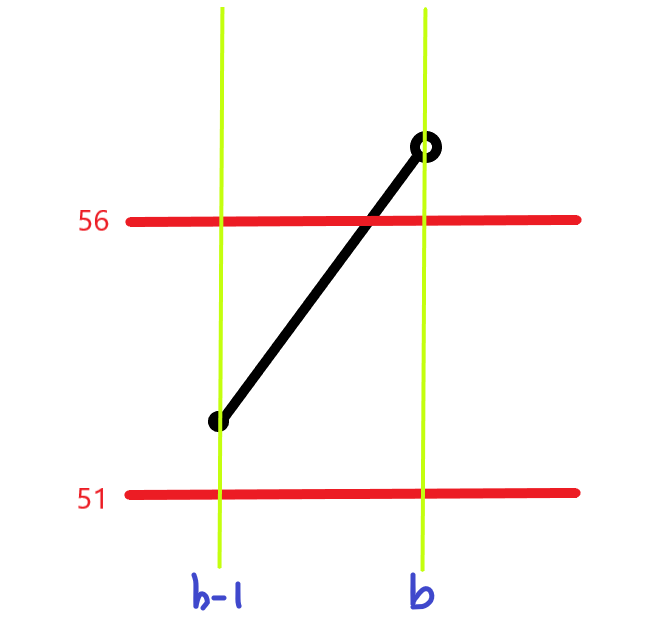
두 식을 연립하자.
따라서
따라서 ii) 에서 가능한 순서쌍은 없다.
i), ii) 를 종합하였을 때 문제에서 말하는
따라서
625
위와 같이 비슷한 형태의 그래프가 점점 뒷구간으로 가면서 작아지는 형태의 함수..
에서 문제를 내는 경우가 꽤 많이 보인다.
이 문제도 비슷하게 만들었는데, 너무 많이 꼬았나라는 생각이 드는 한편 너무 쉬운 게 아닌가라는 생각도 든다.
여담으로 친구에게 검수를 시켰더니 아무 이상이 없다고 했다.
그런데 다음날 다시 풀어보니 답이 여러 개라는 오류가 발견되어
