코드업 3290 : 최소 비용 신장 트리

문제링크

최소 비용 신장 트리

** MST - KRUSKAL (그리디&유니온 파인드) **

이 문제는 최소 비용 신장 트리를 만든 후 그 중 홀수 가중치의 값들만 구하는 문제이다.

이 때, 우리는 이런 생각을 이끌어낼 수 있다.

가중치를 최종 거리 변수(답)에 더할 때, 홀수인 가중치만 더하자!

됐다. 이제 어느 정도 문제에 대한 구상이 되었으니 본격적으로 문제를 풀어보자.

 

풀이

MST 알고리즘을 이용하되, 가중치를 더할 때 홀수인지만 확인해서 더한다.

 

그렇다면 MST 알고리즘이 뭔지 알아보자.

문제에서도 나와있다시피 MST는 (Minimum Cost Spanning Tree)의 약자이다.

이를 실제 상황에 예를 들어 설명하자면,

톨게이트 A~E가 있다.

또한 톨게이트 A~E는 서로를 잇는 도로 여러개가 있고, 그에 따른 비용(가중치)도 있다.

이 때, 톨게이트 A~E를 모두 잇되(트리로 만든다) 비용이 가장 적게 드는 방향으로 잇는다(가중치의 합이 최소로 되게).

(단, 여기서 거리는 상관하지 않는다.)

 

톨게이트 A~E와 서로를 잇는 도로, 또한 그에 따른 비용까지 나타내어져 있다.

 

 

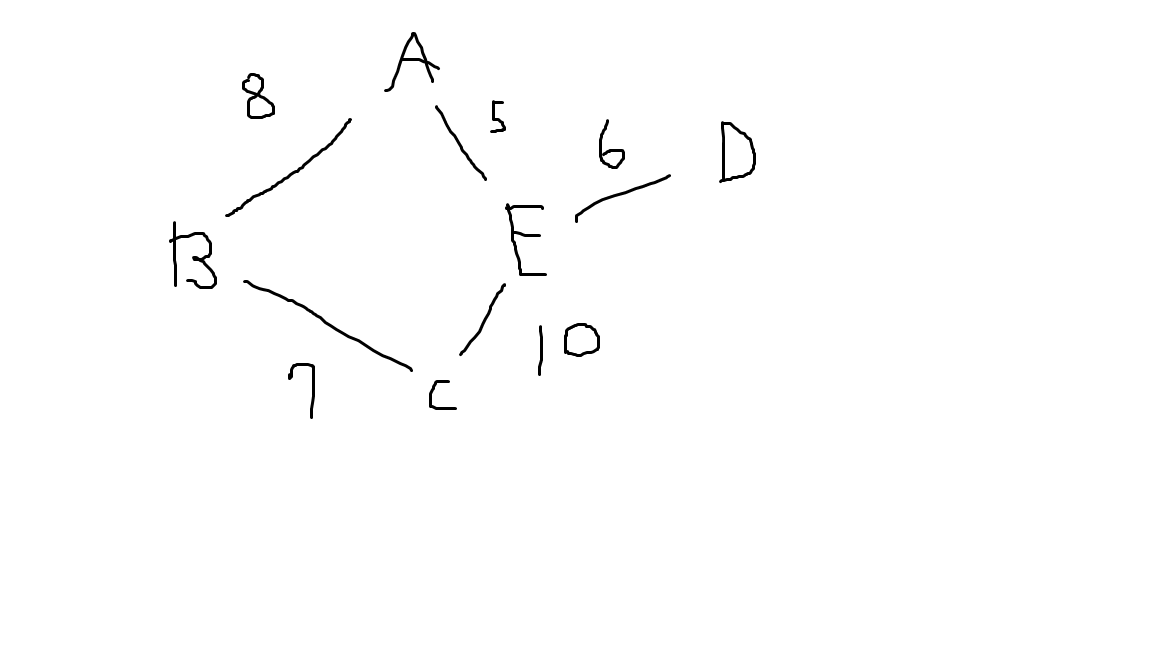
위 그림에는 도로(간선) 5개가 있는데 이 중 톨게이트 갯수-1(n-1)개의 도로(간선)를 '잘' 선택해서

어느 톨게이트에서 출발하더라도 어느 톨게이트에 도착할 수 있게 도로를 만들되 드는 비용이 가장 적어야한다.

 

이제 그 '잘' 을 해야 된다.

 

먼저 말로 설명하겠다.

** 최적의 트리의 해는 최적의 그래프의 해보다 가중치의 합이 무조건 더 작기 때문에 답이 그래프가 되어서는 안된다 **

일단 부모배열을 만든다.

최초에 모든 노드의 부모 노드는 자기 노드이다.

그러므로 반복문으로 V[I]=I; 라는 작업을 해준다.

 

그 다음 가장 가중치의 값이 적은 구간을 택하고 잇는다. (중복 상관X)

이제 A와 E는 이어졌다. 이를 "E는 A에 속해있다" 라는 뜻으로 V[5]=1; (여기서 5는 E를 나타내는 것이고, 1은 A를 나타내는 것이다. 알파벳순)

원래 부모배열에는 1,2,3,4,5가 있었는데 E가 A에 속하게 되면서 V[5]=1 이 되었다

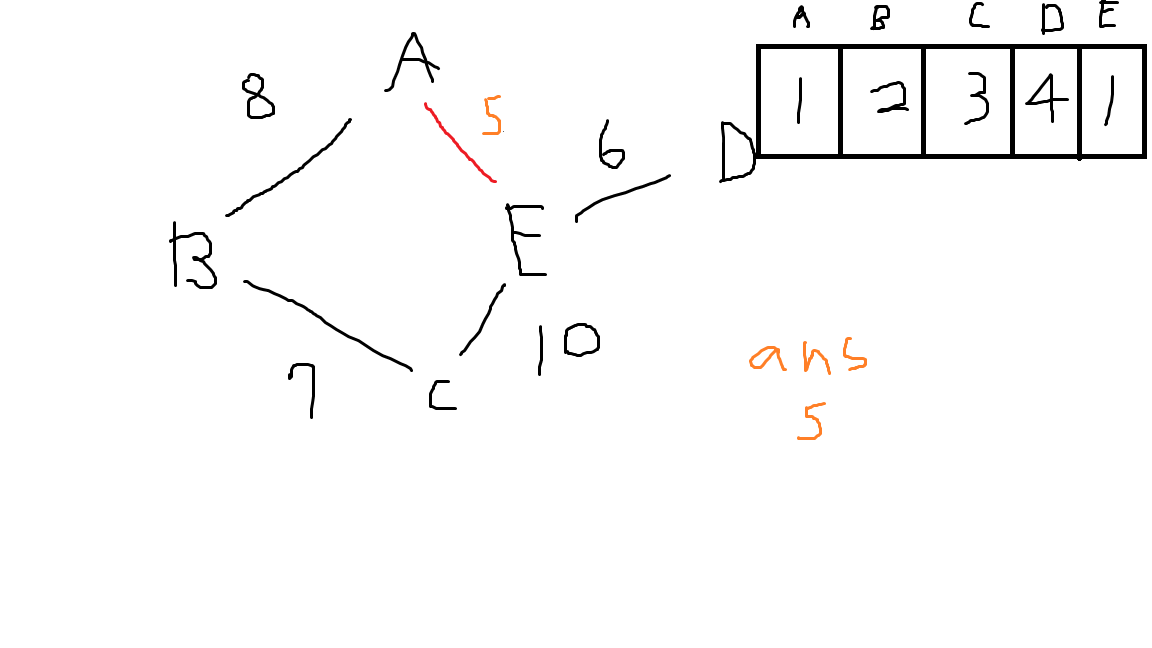
그 다음으로 작은 가중치는 6이다. D와 E를 잇자.

여기서 D가 속한 트리의 루트노드(D의 부모의 부모의부모의부모의...부모)는 D이다.

E가 속한 트리의 루트노드는 A이다. 값 상으로 A < D 이므로 D가 A에 속한다고 하자.

그러면 V[4]=1 이 될 것이다. 또한 가중치 6을 ans에다가 더한다.

D와 E를 이엇다. D의 루트(D)는 E의 루트(A)에 속했고 ans에는 가중치 6이 더해졌다.

이제 그 다음으로 작은 가중치는 7이다.

그래서 B와 C를 잇는다.

B의 루트 B와 C의 루트 C 중 값 상으로 더 작은 것은 B이므로 "C가 B에 속한다"라고 할 것이다.

V[3]=2가 될 것이며 ans에는 7이 더해질 것이다.

B와 C가 이어졌다. C의 루트는 B의 루트의 속해졌으며 ans에는 가중치의 값인 7이 더해졌다.

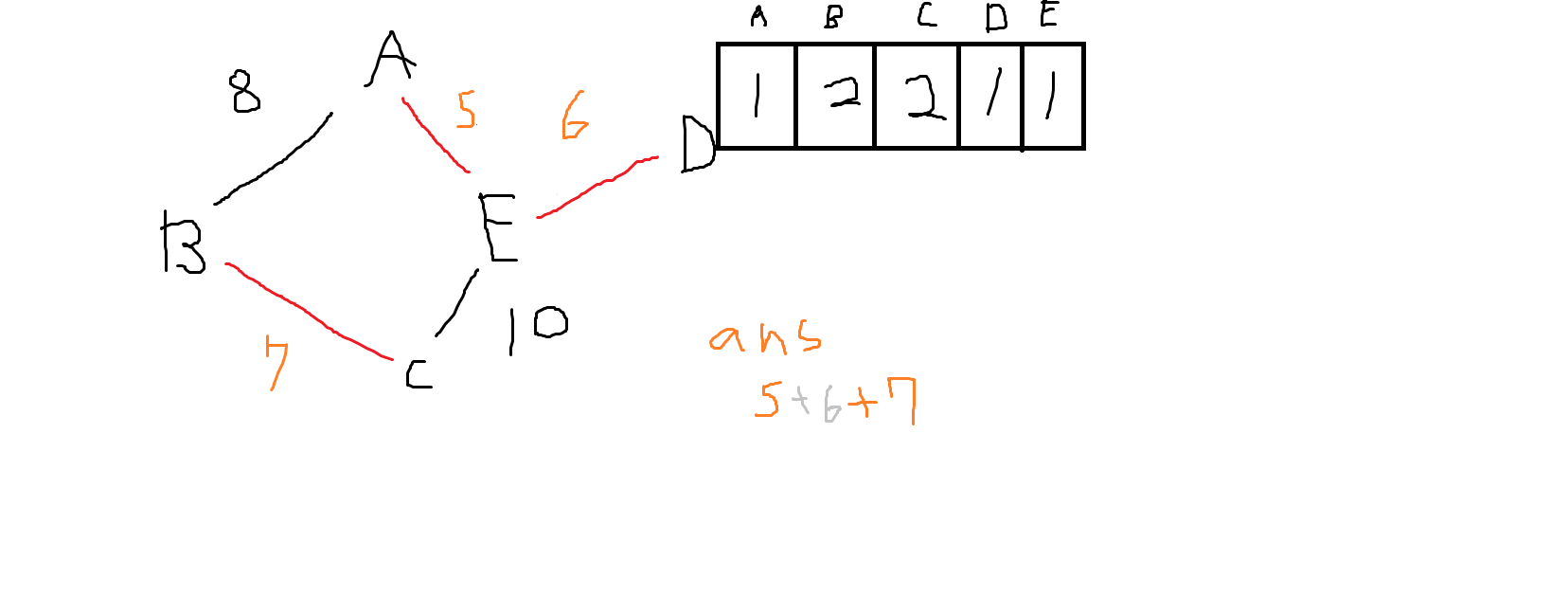
마찬가지로 이제 A와 B를 잇는다.

A의 루트(A) < B의 루트(B) 이기 때문에 V[B의 루트]=V의 루트 => V[B]=A => V[2]=1 을 해준다.

그리고 ans에다가 가중치 8도 더해준다.

A와 B가 이어졌다.

사실 최소 비용 스패닝 트리는 완성이 되었지만 탐색은 남아있다.

바로 C와 E를 잇는 비용 10의 간선이다.

C의 루트와 E의 루트를 보겠다.

C의 루트(부모의 부모의 부모의 부모...의 부모)는 결과적으로 A이다. (C의 부모는 B인데 B의 부모가 A이기 때문. 참고로 A의 부모는 A이다)

E의 루트는 A다.

 

이 뜻은 C는 A에 속한다. E도 A에 속한다. 라는 뜻이다.

결국 둘의 루트 노드는 같다.

이 말을 바꿔 말하면, C부터 A는 연결되어 있다. E와 A는 연결되어있다.

그러면 C와 E는 연결되어있다?

그렇다. C와 E는 이미 연결되어 있으므로 여기서 또 연결해버리면 싸이클이 생기면서 트리가 아니게 된다.

그래서 스킵한다.

 

C와 E는 이미 다른 길로 연결되어있기 떄문에 연결하면 안 된다.

이로써 탐색이 끝났다.

이제 지금까지 ans에 더해온 수를 보자.

5와 7은 홀수라서 더했지만, 6과 8은 짝수라서 더하지 않았다.

ans는 12가 되고, 위 그림과 같게 입력된다면, 출력은 12가 맞게 된다.

 

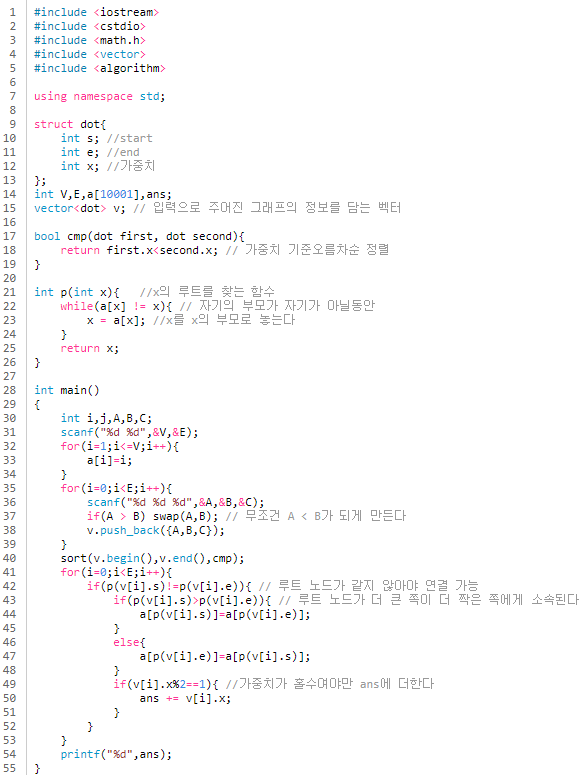
지금까지 말한 내용을 코드로 정리하자면 다음과 같다.

어려운 내용은 아니니 이해하였으면 좋겠다.